Temat 11. Opracować arkusz kalkulacyjny wyznaczający dodatkowe tłumienie związane z opadami metodą Crane'a.
1. Opis modelu
Model Crane’a, zaproponowany przez Roberta K. Crane’a w 1980 roku, to powszechnie stosowany model predykcyjny do oszacowania tłumienia sygnału radiowego spowodowanego opadami deszczu. Przewidywania są możliwe zarówno dla naziemnych tras transmisji (tzw. torów naziemnych - poziomych), jak i dla połączeń z satelitami (tzw. torów satelitarnych lub skośnych - pionowych). Model ten jest zbudowany na podstawie empirycznych obserwacji geofizycznych, które obejmują intensywność punktową opadów, strukturę przestrzenną opadów, a także pionowy rozkład temperatury atmosferycznej.
Wartość tłumienia zależy od kilku kluczowych czynników, takich jak intensywność opadów (wyrażona w mm/h), częstotliwość sygnału oraz długość trasy transmisyjnej. W modelu Crane’a uwzględnia się również zmienność przestrzenną i czasową opadów oraz ich rozkład w pionie, co pozwala na lepsze odwzorowanie rzeczywistego wpływu deszczu na tłumienie sygnału. Model szczegółowo opisuje tłumienie specyficzne, czyli tłumienie przypadające na jednostkę długości toru (zwykle w dB/km), oraz efektywną długość toru, która różni się w zależności od rodzaju połączenia (naziemnego lub satelitarnego). Metoda Crane’a jest w stanie przewidzieć tłumienie dla wybranych wartości procentowych roku, co pozwala oszacować ryzyko tłumienia przekraczającego określony poziom dla konkretnego obszaru.
2. Metoda obliczeniowa
W metodzie tej wyróżnia się trzy zakresy dystansu \( D \), gdzie:
- dla dystansów krótszych niż odległość graniczna \( d \) stosuje się uproszczony wzór,
- dla dystansów mieszczących się w przedziale \( d \leq D \leq 22.5 \, \text{km} \) stosuje się pełny wzór uwzględniający szczegółowy rozkład tłumienia,
- dla dystansów większych niż 22.5 km stosuje się efektywne prawdopodobieństwo przekroczenia \( P' \).
2.1. Całkowite tłumienie deszczowe dla krótkich dystansów
Dla dystansów mieszczących się w przedziale \( d \leq D \leq 22.5 \, \text{km} \), całkowite tłumienie deszczowe \( A_R \) oblicza się z użyciem następującego wzoru:
\( A_R = k R_p^{\alpha} \left( \frac{e^{\mu \alpha d} - 1}{\mu \alpha} - \frac{b^{\alpha} e^{c \alpha d}}{c \alpha} + \frac{b^{\alpha} e^{c \alpha D}}{c \alpha} \right) \)
gdzie:
- \( A_R \) - całkowite tłumienie deszczowe (w dB),
- \( k \) oraz \( \alpha \) - współczynniki zależne od częstotliwości i polaryzacji sygnału,
- \( R_p \) - intensywność opadów (w mm/h),
- \( D \) - długość toru transmisyjnego (w km),
- \( d \) - charakterystyczna odległość graniczna wyznaczona przez model Crane’a,
- \( \mu \), \( b \), oraz \( c \) - współczynniki wyliczane według poniższych wzorów.
Obliczenia współczynników
Wartości parametrów \( \mu \), \( b \), \( c \), oraz \( d \) oblicza się na podstawie intensywności deszczu \( R_p \) za pomocą następujących wzorów:
\( \mu = \frac{\ln(b e^{c d})}{d} \)
\( b = 2.3 R_p^{-0.17} \)
\( c = 0.026 - 0.03 \ln(R_p) \)
\( d = 3.8 - 0.6 \ln(R_p) \)
Opis współczynników
-
Współczynnik \( b \):
Jest to współczynnik skalowania przestrzennego, który jest związany z intensywnością opadów. Wyższe wartości \( R_p \) (intensywności opadów) zmniejszają wartość \( b \), co oznacza, że sygnał tłumi się bardziej gwałtownie na krótszych dystansach.
-
Współczynnik \( c \):
Jest to współczynnik zanikania intensywności, który opisuje zanikanie intensywności tłumienia w miarę zwiększania się odległości. Im niższa wartość \( c \), tym bardziej trwałe jest tłumienie na większych dystansach, co odpowiada intensywniejszym opadom.
-
Odległość graniczna \( d \):
Jest to odległość charakterystyczna, po przekroczeniu której tłumienie osiąga swoją maksymalną stabilizację. Niższe wartości \( d \) (wynikające z wyższych wartości \( R_p \)) oznaczają, że maksymalne tłumienie występuje na krótszych dystansach.
-
Współczynnik \( \mu \):
Jest to współczynnik modyfikacji, który uwzględnia zmienność intensywności opadów wzdłuż trasy transmisyjnej, dostosowując tłumienie do faktycznych warunków atmosferycznych.
2.2. Całkowite tłumienie dla mniejszych dystansów
Jeśli długość toru transmisyjnego \( D \) jest mniejsza niż odległość graniczna \( d \), stosuje się uproszczony wzór dla tłumienia:
\( A_R = k R_p^{\alpha} \left( \frac{e^{\mu \alpha d} - 1}{\mu \alpha} \right) \)
2.3. Całkowite tłumienie dla dystansów większych niż 22.5 km
Jeśli długość toru transmisyjnego \( D \) przekracza 22.5 km, stosujemy skalowanie prawdopodobieństwa przekroczenia, aby uzyskać efektywne prawdopodobieństwo \( P' \):
\( P' = \frac{22.5}{D} \cdot P \)
Obliczone \( P' \) oznacza efektywne prawdopodobieństwo przekroczenia dla toru o długości 22.5 km. Po wyliczeniu \( P' \), używamy go do odczytania intensywności opadów \( R_p \) z tabeli intensywności opadów, wybierając wartość odpowiadającą najbliższemu procentowi przekroczenia w tabeli.
Odczytane w ten sposób \( R_p \) następnie stosujemy w standardowym wzorze na tłumienie Crane’a, zakładając długość toru jako 22.5 km:
\( A_R = k R_p^{\alpha} \left( \frac{e^{\mu \alpha d} - 1}{\mu \alpha} - \frac{b^{\alpha} e^{c \alpha d}}{c \alpha} + \frac{b^{\alpha} e^{c \alpha D}}{c \alpha} \right) \)
Ta metoda pozwala na uwzględnienie wpływu deszczu na większych dystansach bez przeszacowania tłumienia, dzięki redukcji efektywnego dystansu do 22.5 km.
Tabela 1: Wartości współczynników \( k_H \), \( k_V \), \( \alpha_H \), \( \alpha_V \) dla różnych częstotliwości
Instrukcja korzystania: Aby użyć tej tabeli, wybierz odpowiednie wartości współczynników \( k_H \), \( k_V \), \( \alpha_H \), \( \alpha_V \) w zależności od częstotliwości sygnału oraz polaryzacji (pozioma lub pionowa). Następnie podstaw te wartości do wzoru na tłumienie, aby uzyskać wynik dla określonej konfiguracji transmisyjnej.
| Frequency (GHz) | kH | kV | αH | αV |
|---|---|---|---|---|
| 1 | 0.0000387 | 0.0000352 | 0.912 | 0.88 |
| 2 | 0.00154 | 0.000138 | 0.963 | 0.923 |
| 4 | 0.00065 | 0.000591 | 1.121 | 1.075 |
| 6 | 0.00175 | 0.00155 | 1.308 | 1.265 |
| 7 | 0.00301 | 0.00265 | 1.332 | 1.312 |
| 8 | 0.00454 | 0.00395 | 1.327 | 1.31 |
| 10 | 0.0101 | 0.00887 | 1.276 | 1.264 |
| 12 | 0.0188 | 0.0168 | 1.217 | 1.2 |
| 15 | 0.0367 | 0.0335 | 1.154 | 1.128 |
| 20 | 0.0751 | 0.0691 | 1.099 | 1.065 |
| 25 | 0.124 | 0.113 | 1.061 | 1.03 |
| 30 | 0.187 | 0.167 | 1.021 | 1 |
| 35 | 0.263 | 0.233 | 0.979 | 0.963 |
| 40 | 0.35 | 0.31 | 0.939 | 0.929 |
| 45 | 0.442 | 0.393 | 0.903 | 0.897 |
| 50 | 0.536 | 0.479 | 0.873 | 0.868 |
| 60 | 0.707 | 0.642 | 0.826 | 0.824 |
| 70 | 0.851 | 0.784 | 0.793 | 0.793 |
| 80 | 0.975 | 0.906 | 0.769 | 0.769 |
| 90 | 1.06 | 0.999 | 0.753 | 0.754 |
| 100 | 1.12 | 1.06 | 0.743 | 0.744 |
Tabela 2: Intensywność opadów (mm/h) dla regionów A-H
Instrukcja korzystania: Aby użyć tej tabeli, wybierz odpowiednią wartość intensywności opadów w mm/h dla swojego regionu klimatycznego (A-H) oraz odpowiednie procentowe prawdopodobieństwo przekroczenia w ciągu roku.
- Dla wysokiej niezawodności (aby uwzględnić rzadkie, intensywne opady) wybierz niski procent przekroczenia, np. 0.001% lub 0.01%.
- Dla przeciętnej niezawodności wybierz wyższy procent przekroczenia, np. 0.1% lub 1%.
Wybrana wartość będzie pełniła rolę \( R_p \) w obliczeniach tłumienia deszczowego w modelu Crane'a.
| % of year exceeded | A | B | B1 | B2 | C | D1 | D2 | D3 | E | F | G | H |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.001 | 28.1 | 52.1 | 42.6 | 63.8 | 71.6 | 86.6 | 114.1 | 133.2 | 176.0 | 70.7 | 197.0 | 542.6 |
| 0.002 | 20.9 | 41.7 | 32.7 | 50.9 | 58.9 | 69.0 | 88.3 | 106.6 | 145.4 | 50.4 | 159.6 | 413.9 |
| 0.003 | 17.5 | 36.1 | 27.8 | 43.8 | 50.6 | 60.4 | 75.6 | 93.5 | 130.0 | 41.4 | 140.8 | 350.3 |
| 0.005 | 13.8 | 29.2 | 22.3 | 35.7 | 41.4 | 49.2 | 62.1 | 78.7 | 112.0 | 31.9 | 118.0 | 283.4 |
| 0.01 | 9.9 | 21.1 | 16.1 | 25.8 | 29.5 | 36.2 | 46.8 | 61.6 | 91.5 | 22.2 | 90.2 | 209.3 |
| 0.02 | 6.9 | 14.6 | 11.3 | 17.6 | 19.9 | 25.4 | 34.7 | 47.0 | 72.2 | 15.0 | 66.8 | 152.4 |
| 0.03 | 5.5 | 11.6 | 9.0 | 13.9 | 15.6 | 20.3 | 28.6 | 39.9 | 62.4 | 11.8 | 55.8 | 125.9 |
| 0.05 | 4.0 | 8.6 | 6.8 | 10.3 | 11.5 | 15.3 | 22.2 | 31.6 | 50.4 | 8.5 | 43.8 | 97.2 |
| 0.1 | 2.5 | 5.7 | 4.5 | 6.8 | 7.7 | 10.3 | 15.1 | 22.4 | 36.2 | 5.3 | 31.3 | 66.5 |
| 0.2 | 1.5 | 3.8 | 2.9 | 4.4 | 5.2 | 6.8 | 9.9 | 15.2 | 24.1 | 3.1 | 22.0 | 43.5 |
| 0.3 | 1.1 | 2.9 | 2.2 | 3.4 | 4.1 | 5.3 | 7.6 | 11.8 | 18.4 | 2.2 | 17.7 | 33.1 |
| 0.5 | 0.5 | 2.0 | 1.5 | 2.4 | 2.9 | 3.8 | 5.3 | 8.2 | 12.6 | 1.4 | 13.2 | 22.6 |
| 1 | 0.2 | 1.2 | 0.8 | 1.4 | 1.8 | 2.2 | 3.0 | 4.6 | 7.0 | 0.6 | 8.4 | 12.4 |
| 2 | 0.1 | 0.5 | 0.4 | 0.7 | 1.1 | 1.2 | 1.5 | 2.0 | 3.3 | 0.2 | 5.0 | 5.8 |
| 3 | 0.0 | 0.3 | 0.2 | 0.4 | 0.6 | 0.6 | 0.9 | 0.8 | 1.8 | 0.1 | 3.4 | 3.3 |
| 5 | 0.0 | 0.2 | 0.1 | 0.2 | 0.2 | 0.2 | 0.3 | 0.0 | 0.2 | 0.1 | 1.8 | 1.1 |
Obraz 1: Mapa świata przedstawiająca regiony deszczowe Crane'a z 1996 roku
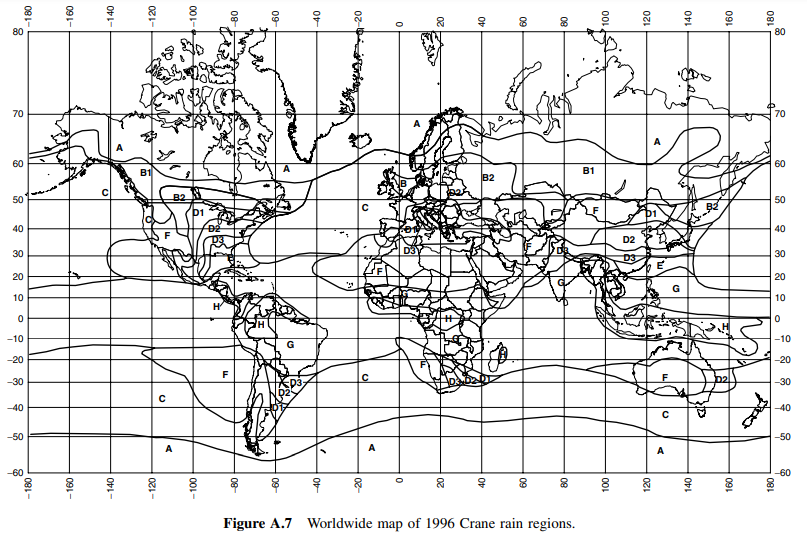
3. Zadanie projektowe
Wyznaczyć tłumienie dla wybranej przykładowej trasy o długości 25km położonej w północnej i południowej części Polski dla dwóch różnych częstotliwości (poniżej i powyżej 10GHz)
Obliczenia zostaną wykonane dla Olsztyna oraz Krakowa.
Na podstawie analizy map IMGW, które ukazują maksymalną dobową sumę opadów atmosferycznych w 3 dekadach każdego miesiąca o prawdopodobieństwie wystąpienia 1%, wybrano maksymalną wartość dla obu miast, a następnie podzielono ją na 24 w celu obliczenia opadu w mm/h.
Dla Olsztyna maksymalny dobowy opad zanotowano w trzeciej dekadzie czerwca, pierwszej i drugiej dekadzie lipca oraz w pierwszej i drugiej dekadzie sierpnia i wynosił on 40mm/dobę, co daje opad około 1,67mm/h. Wartość ta odpowiada regionowi C zgodnie z tabelą intensywności opadów Crane'a.
Dla Krakowa maksymalny dobowy opad zanotowano w w drugiej dekadzie lipca i wynosił on 55mm/dobę, co daje opad około 2,29mm/h. Wartość ta odpowiada regionowi D1 zgodnie z tabelą intensywności opadów Crane'a.
Wyniik obliczeń
Olsztyn - dane przyjęte w obliczeniach:
- Region: C
- Częstotliwość: 4 GHz
- Prawdopodobieństwo: 0.01 %
- Droga: 25 km
Obliczone tłumienie: 0.379 dB
- Region: C
- Częstotliwość: 80 GHz
- Prawdopodobieństwo: 0.01 %
- Droga: 25 km
Obliczone tłumienie: 198.9155 dB
Kraków - dane przyjęte w obliczeniach:
- Region: D1
- Częstotliwość: 4 GHz
- Prawdopodobieństwo: 0.01 %
- Droga: 25 km
Obliczone tłumienie: 0.436 dB
- Region: D1
- Częstotliwość: 80 GHz
- Prawdopodobieństwo: 0.01 %
- Droga: 25 km
Obliczone tłumienie: 217.9022 dB
Wykres zależności tłumienia od częstotliwości dla Olsztyna i Krakowa
Dane: D=25km, P=0,01%
Wykres zależności tłumienia od odległości dla Olsztyna i Krakowa
Dane: f=4GHz, P=0,01%
Wykres zależności tłumienia od odległości dla Olsztyna i Krakowa - 80 GHz
Dane: f=80GHz, P=0,01%
4. Podsumowanie analizy dla Olsztyna i Krakowa
-
Analiza wpływu opadów i częstotliwości na tłumienie sygnału
Na podstawie przeprowadzonych obliczeń można zauważyć znaczący wpływ częstotliwości sygnału na poziom tłumienia deszczowego. W przypadku częstotliwości 80 GHz tłumienie dla obu miast wzrasta o setki decybeli, co oznacza, że tak wysoka częstotliwość jest bardziej narażona na zakłócenia atmosferyczne. Z kolei przy częstotliwości 4 GHz tłumienie jest znacznie niższe, co pozwala na stabilniejsze połączenia w warunkach intensywnych opadów.
-
Porównanie tłumienia w Krakowie i Olsztynie
Wykonane obliczenia i wizualizacje wskazują, że tłumienie sygnału jest wyższe w Krakowie niż w Olsztynie przy obu analizowanych częstotliwościach. Wyższe wartości tłumienia dla Krakowa wynikają z bardziej intensywnych opadów charakterystycznych dla regionu południowej Polski, przypisanego do wyższego regionu deszczowego (D1) według klasyfikacji Crane’a. Olsztyn, należący do regionu C, wykazuje niższe tłumienie, co świadczy o mniej wymagających warunkach atmosferycznych w północnej części kraju.
5. Podsumowanie Projektu
Projekt ten pozwolił na szczegółowe przeanalizowanie tłumienia sygnału radiowego spowodowanego opadami atmosferycznymi, z wykorzystaniem modelu Crane’a dla dwóch polskich miast o różnych warunkach klimatycznych. Wykonane obliczenia dla Olsztyna i Krakowa, przy częstotliwościach 4 GHz oraz 80 GHz, umożliwiły ocenę wpływu opadów na jakość transmisji radiowej. W rezultacie wykazano, że zarówno wyższa częstotliwość, jak i intensywniejsze opady powodują wyższe tłumienie sygnału, co w konsekwencji może ograniczać zasięg i stabilność połączenia. Opracowanie arkusza kalkulacyjnego oraz analiza wizualna wykresów dla różnych scenariuszy tłumienia stanowi solidne narzędzie wspomagające decyzje dotyczące projektowania systemów transmisji radiowej i ich niezawodności w obszarach o różnych profilach klimatycznych.
6. Źródła
- Anderson H. – *Fixed Broadband Wireless System Design*, rozdział 4.3.1 Crane R.
- IEEE Transactions on Communications, Vol. COM-28, No. 9, September 1980